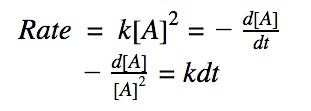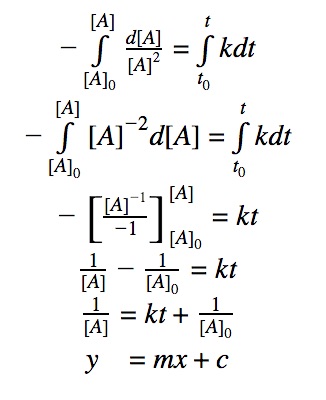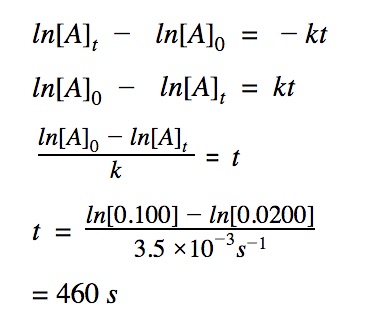Overview
There are two types of rate laws that we need to learn for AP chemistry:
- (1) Differential rate law
- (2) Integrated rate law
What is the difference between the differential rate law and integrated rate law? The differential rate law is actually a derivative of the integrated rate law. In experiments:
- Differential rate law requires measuring initial rate of thereaction when different reactant concentrations are present.
- On the other hand, integrated rate law experiments involve tracking the concentration of a reactant as it decreases over time,with other reactant concentrations remaining relatively constant. This usually occurs over a larger span of time going over more than 2 half-lives. An example of the use of this rate law is to determine low long it would take for a radioactive material to decay to a safe level.
Intergrated rate law
CED Objective: Identify the rate law expression of a chemical reaction using data that show how the concentrations of reaction species change over time.
In this section, we will look at the integration of 1st, 2nd and 0th order reactions and some interesting graphs that the integration produces.
*In AP chemistry, you do not need to know how to derive the rate law expression, but knowing the math behind helps to understand the underlying principles and assumptions made.
First order reactions
For a first order reaction, we know that the rate of reaction is dependent on one 1st order reactant.
rate = k•[A]
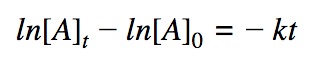
Click to show integration
First order differential rate law:
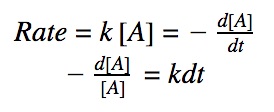
Integrating both sides by time between t=0 and t = t:
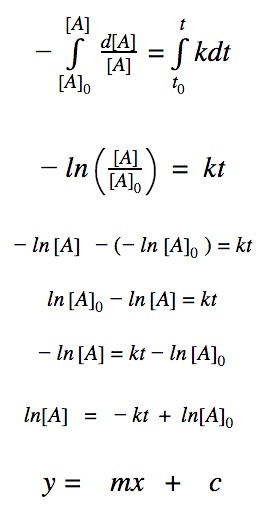
2nd order reactions
For a 2nd order reaction, we know that the rate of reaction is dependent on the square of the reactant’s concentration.
rate = k•[A]²
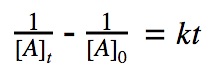
Click to show integration
0th order reactions
A 0th order reaction rate is defined by the decrease in concentration of reactants over time. A zeroth order reaction rate does not depend on the concentration of the reactant, it means that the rate of reaction is constant over time even though the reactants are decreasing as the reaction progresses.
Rate = K
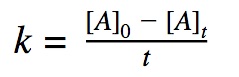
Click to show integration
See how the integrated rate law is derived using calculus.
0th order differential rate law:
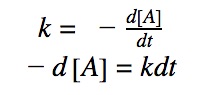
Integrating both sides by time between t=0 and t = t:
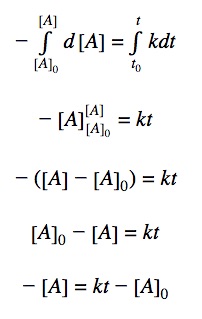
Rearranging the equation:
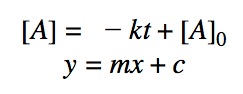
Graphs
The most useful aspect of the integration is to arrive at an equation y = mx + c, as this can be easily graphed. And by distinguishing the patterns of the graphs, we can quickly determine if the reaction is 0th, 1st, or 2nd order.
Comparison of Reaction Orders in Concentration vs. Time Graphs
| Reaction Order | Linear Graph | Characteristics | Rate | Rate Units |
|---|---|---|---|---|
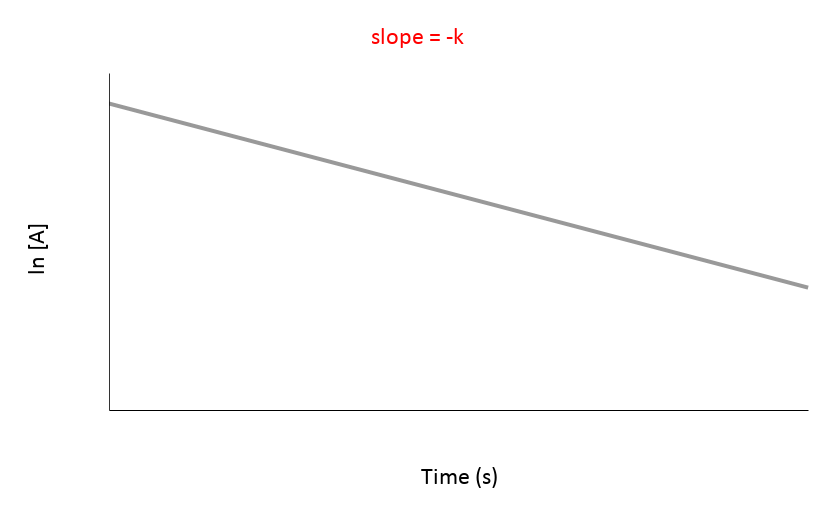
| 1st | ln[A] vs. t | Straight line with a negative slope (-K) | Rate = [A] | mol/(L·s) or M/s |
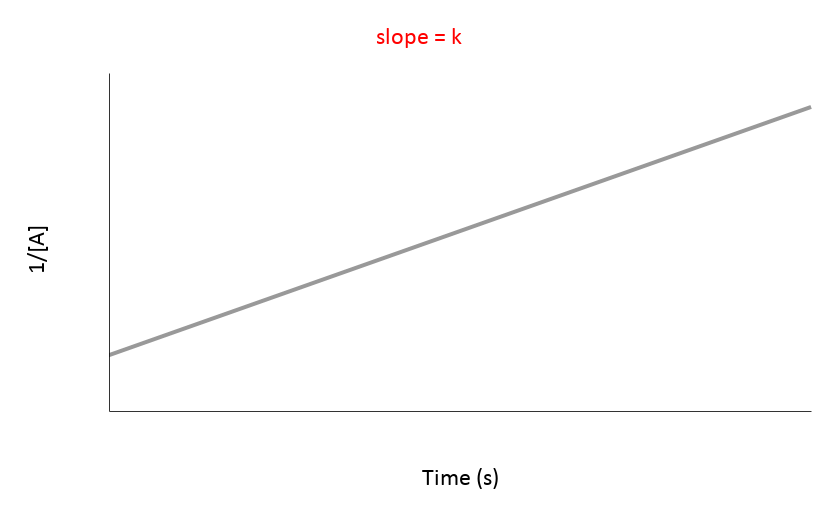
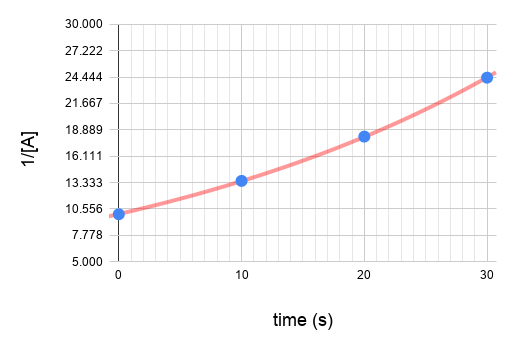
| 2nd | 1/[A] vs. t | Straight line (K) | Rate = [A]² | mol/(L·s) or M/(s·M) |
| 0th | [A] vs. t | Straight line with a negative slope (-K) | Rate = k (constant) | mol/(L·s) or M/s |
These characteristics should help you quickly identify the order of reaction by examining the shape and linearity of the concentration vs. time graph and the relationship between concentration and time.
Example
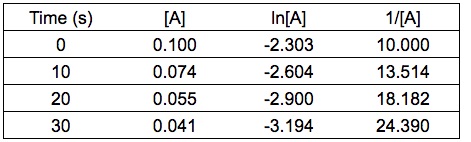
Given the experimental data (see table below), determine the rate law for the reaction with respect to reactant A.
You can determine the order from integrated rate law. Calculate the values of ln[A] and 1/[A] .
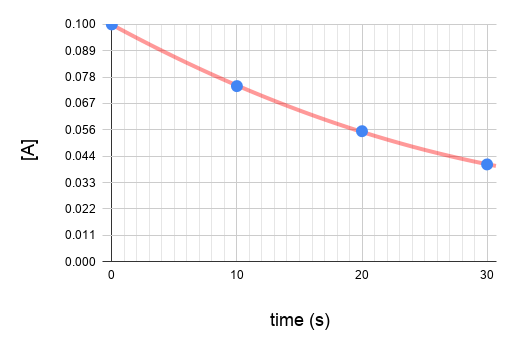
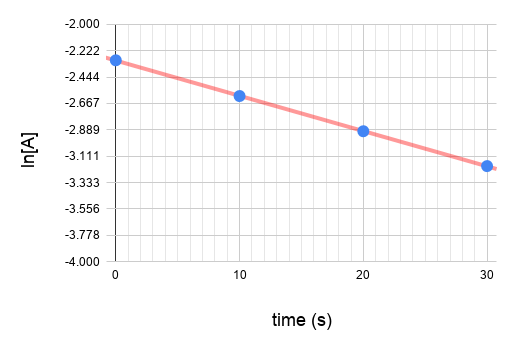
Plot the graphs.
Since graph ln[A] vs time gives a straight line and the others do not, we know that the reaction is a first order reaction with respect to A.
Determine time
How long will it take for the reaction to reach 0.0200 M which has a rate constant of k = 3.5 x 10⁻³ s⁻¹. The initial concentration is 0.100 M.
To determine t, we need to know:
[A]₀ – the initial concentration
[A]t – the final concentration
The order of the reacton
The rate constant k is given 3.5 x 10⁻³ s⁻¹